GreenMaker
Member
- Gender
- Male
- Guildcard
- 42047246
ここでは、
敵のどれだけ倒せばレアが出るのか（＝目標討伐数）について解説します。
※これは確率の計算から求められたものであるため、不確かさを含みます。
レアアイテムは確率の計算に従って出るわけではありません。
飽くまで目安であること、ご了承ください。
敵のどれだけ倒せばレアが出るのか（＝目標討伐数）について解説します。
※これは確率の計算から求められたものであるため、不確かさを含みます。
レアアイテムは確率の計算に従って出るわけではありません。
飽くまで目安であること、ご了承ください。
敵から獲得できるレアアイテムは、
DAR-ドロップ率：敵がアイテム（消費アイテムやメセタなど）を落とす確率
RDR-レアドロップ率：敵がレアアイテムを落とす確率
の積で求められます。
ここでは、これをRAR（Rare Apperance Rate：レア出現率）として定義し、使用していきます。
例えば、難易度アルティメット・ID赤・地下砂漠のピロ・ゴランからは
レアアイテムとしてヘブンストライカー(HS)が落ちます。
この場合
DAR：35%・RDR：0.085%のため、RARは
35 × 0.085 ≒ 0.03%（=1/3343）
となります。
また、DARとRDRは週ボーナスやHBR・運ボーナスによってブーストがかけられます。
これによってRARが上昇します。
上の例で、RBRや週ボーナスによって
DAR:150%・RDR：125%になっていた場合、RARは
35% × 1.5 × 0.085 × 1.25 ≒ 0.056%（＝1/1793）
となります。
DAR-ドロップ率：敵がアイテム（消費アイテムやメセタなど）を落とす確率
RDR-レアドロップ率：敵がレアアイテムを落とす確率
の積で求められます。
ここでは、これをRAR（Rare Apperance Rate：レア出現率）として定義し、使用していきます。
例えば、難易度アルティメット・ID赤・地下砂漠のピロ・ゴランからは
レアアイテムとしてヘブンストライカー(HS)が落ちます。
この場合
DAR：35%・RDR：0.085%のため、RARは
35 × 0.085 ≒ 0.03%（=1/3343）
となります。
また、DARとRDRは週ボーナスやHBR・運ボーナスによってブーストがかけられます。
これによってRARが上昇します。
上の例で、RBRや週ボーナスによって
DAR:150%・RDR：125%になっていた場合、RARは
35% × 1.5 × 0.085 × 1.25 ≒ 0.056%（＝1/1793）
となります。
では、このRARで求められる確率とは何でしょうか？
先の例だと、
DARやRDRに補正がかけられていない場合のHSのRARは1/3343です。
これはピロ・ゴランを1体倒した場合のHSの入手率となります。
ここで注意しておきたいのが確率の計算は加算ではないことです。（よく勘違いしやすいので注意！）
ピロゴランを2体倒した場合、HSの入手率は 1/3343 + 1/3343 = 2/3343 となるわけではありません。
ピロ・ゴランを2体倒した場合の確率は、2体倒してもレアアイテムが出ない確率の余事象であるため
1 - (1-1/3343) ^ 2 ≒ 0.0595%
となります。
この式を一般化してみます。
RARがAの確率である敵をN体倒した場合の入手率Rは
R = 1 ÷ (1 - (1-A) ^ N) ー（１）
となります。
先の例だと、
DARやRDRに補正がかけられていない場合のHSのRARは1/3343です。
これはピロ・ゴランを1体倒した場合のHSの入手率となります。
ここで注意しておきたいのが確率の計算は加算ではないことです。（よく勘違いしやすいので注意！）
ピロゴランを2体倒した場合、HSの入手率は 1/3343 + 1/3343 = 2/3343 となるわけではありません。
簡単な例を一つあげます。
六面サイコロで1の目を出す遊びをするとします。
各目の出る確率は一様に1/6です。
だからと言って、サイコロを6回振れば1回は必ず1の目が出るとは限りません。
では、サイコロを6回振った場合
少なくとも1回、1の目が出る確率Rはいくらなのでしょうか？
答えは少なくとも1回という部分に隠されてます。
これは、
「1以外（2～6）の目を連続で6回引けば
1回も1が出ないことになるため、それが起こらないこと」
と言い換えることができます。
1以外の目が出る確率は
1 - 1/6 = 5/6
であり、6回の試行はそれぞれ独立しているため、Rは
1 - ( 5/6) ^ 6= 31031/46656（≒66.7%）
となります。
これを余事象の考え方といいます。
「6回連続で引く」は1以外の目を引く確率（=余事象）のべき乗（今回は6乗）に充てられ、
それを「起こらなくする」ため全体：100％=1から減算するという計算です。
六面サイコロで1の目を出す遊びをするとします。
各目の出る確率は一様に1/6です。
だからと言って、サイコロを6回振れば1回は必ず1の目が出るとは限りません。
では、サイコロを6回振った場合
少なくとも1回、1の目が出る確率Rはいくらなのでしょうか？
答えは少なくとも1回という部分に隠されてます。
これは、
「1以外（2～6）の目を連続で6回引けば
1回も1が出ないことになるため、それが起こらないこと」
と言い換えることができます。
1以外の目が出る確率は
1 - 1/6 = 5/6
であり、6回の試行はそれぞれ独立しているため、Rは
1 - ( 5/6) ^ 6= 31031/46656（≒66.7%）
となります。
これを余事象の考え方といいます。
「6回連続で引く」は1以外の目を引く確率（=余事象）のべき乗（今回は6乗）に充てられ、
それを「起こらなくする」ため全体：100％=1から減算するという計算です。
ピロ・ゴランを2体倒した場合の確率は、2体倒してもレアアイテムが出ない確率の余事象であるため
1 - (1-1/3343) ^ 2 ≒ 0.0595%
となります。
この式を一般化してみます。
RARがAの確率である敵をN体倒した場合の入手率Rは
R = 1 ÷ (1 - (1-A) ^ N) ー（１）
となります。
（１）の式はその性質上、
Nをいくら上げてもRを1(＝100%）にすることはできません。
先程のサイコロの例を出すと、
サイコロを10回振っても1が一度も出ないことはあります。
50回振っても出ないこともあり得るわけです。
ただ、50回振っても出ないことはあるとはいえ、
そのようなことはほとんど起こらないように思えます。
サイコロを50回振って一度も1が出ない確率は0.01%であり
そのようなことがほぼ起こらないと言ってよいでしょう。
この「ほぼ」に当たる部分はどこまで許容すればよいのでしょうか。
統計学的には、95%信頼区間という用語があります。
詳しい解説は省きますが、95%は統計学上信頼できる値とされています。
レア周回の場合、レアが出るまでの討伐数を真値と定義すれば
その真値が統計学的に5%から外れることを「運が悪い」と判断します。
この95%信頼区間の考え方を先程の余事象の式に対応させます。
（１）の式にR=95%を代入すると
1 - (1-A)^N = 0.95
となります。
これは、RAR=Aの敵をN回倒した場合、レアアイテムの入手率が95%になることを示しています。
この式をNについて解くと
N = log((1-A) , 0.05)
となります。
このNは入手率が95%になるまで敵を倒した数ということができます。
Nを目標討伐数と呼ぶこととします。
Nをいくら上げてもRを1(＝100%）にすることはできません。
先程のサイコロの例を出すと、
サイコロを10回振っても1が一度も出ないことはあります。
50回振っても出ないこともあり得るわけです。
ただ、50回振っても出ないことはあるとはいえ、
そのようなことはほとんど起こらないように思えます。
サイコロを50回振って一度も1が出ない確率は0.01%であり
そのようなことがほぼ起こらないと言ってよいでしょう。
この「ほぼ」に当たる部分はどこまで許容すればよいのでしょうか。
統計学的には、95%信頼区間という用語があります。
詳しい解説は省きますが、95%は統計学上信頼できる値とされています。
レア周回の場合、レアが出るまでの討伐数を真値と定義すれば
その真値が統計学的に5%から外れることを「運が悪い」と判断します。
この95%信頼区間の考え方を先程の余事象の式に対応させます。
（１）の式にR=95%を代入すると
1 - (1-A)^N = 0.95
となります。
これは、RAR=Aの敵をN回倒した場合、レアアイテムの入手率が95%になることを示しています。
この式をNについて解くと
N = log((1-A) , 0.05)
となります。
このNは入手率が95%になるまで敵を倒した数ということができます。
Nを目標討伐数と呼ぶこととします。
目標討伐数Nは自然対数を用いた数であり、
手計算で求めるのは難しいです。
どうにかして目標討伐数を簡単に求める方法は見つけられないでしょうか？
下に、赤ピロ・ゴランのRARとブースト値における目標討伐数を示します。
この表では
目標討伐数をブースト後のRARの分母で割るとおよそ3になります。
これはブーストが乗っている場合も同様です。
つまり、ブースト後のRARの分母に3を掛けた値がおおよその目標討伐数になります。
手計算で求めるのは難しいです。
どうにかして目標討伐数を簡単に求める方法は見つけられないでしょうか？
下に、赤ピロ・ゴランのRARとブースト値における目標討伐数を示します。
この表では
目標討伐数をブースト後のRARの分母で割るとおよそ3になります。
これはブーストが乗っている場合も同様です。
つまり、ブースト後のRARの分母に3を掛けた値がおおよその目標討伐数になります。
目標討伐数を求めた後、
クエストでの敵の出現数で割れば必要な周回回数を求めることができます。
さらに、周回にかかる時間が分かっていれば、
目標討伐数を達成するまでにかかる時間を求めることが可能です。
マルチの場合は、人が集まるまでの時間も計算に入れておきましょう。
クエストでの敵の出現数で割れば必要な周回回数を求めることができます。
さらに、周回にかかる時間が分かっていれば、
目標討伐数を達成するまでにかかる時間を求めることが可能です。
例として赤ピロゴランからHSの獲得を考えます。
ブーストがない場合の必要討伐数は10013体、
周回クエストとして新掃討作戦第三号（NMU3）を想定すると、
当クエストではピロ・ゴランは55体出現するため
必要な周回回数は
10013 ÷ 55 ≒ 183回
1回の周回に15分かかるとすれば、必要な時間は
183 × 15 ≒ 2745分 ≒ 46時間
となります。
この周回時間をさらに縮められれば
その分入手に必要な時間は減ります。
通常のクエストでは敵の湧きや部屋の構造は固定化されているため
次に何が出るか、どこで戦えばよいかなどを把握しておくと
スムーズに進められます。このゲームの醍醐味ですね。
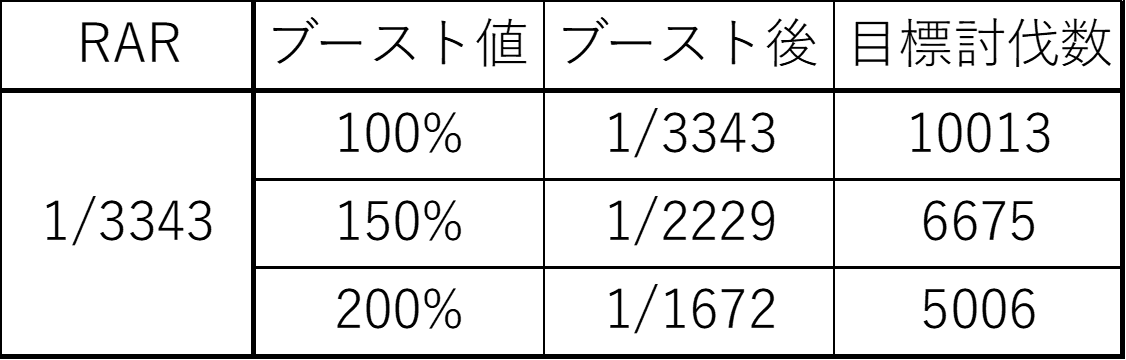
また、RBRや週ブーストによってDARやRDRが増加している場合は
その分必要討伐数が割引されます。
DARが150%、RDRが125%のブーストがかかっている場合、RARは
150% × 125% = 187.5% のブーストがかかるため、
NMU3における周回回数もその分割引され
1つのHS獲得にかかる時間は
46 ÷ 187.5% ≒ 24.5時間 となります。
基本的にRBRではこれらのブーストによって
RBR選出外の優秀なクエストに対抗することが可能となっています。
（中には対抗できない内容のクエストもあるため注意）
ブーストがない場合の必要討伐数は10013体、
周回クエストとして新掃討作戦第三号（NMU3）を想定すると、
当クエストではピロ・ゴランは55体出現するため
必要な周回回数は
10013 ÷ 55 ≒ 183回
1回の周回に15分かかるとすれば、必要な時間は
183 × 15 ≒ 2745分 ≒ 46時間
となります。
この周回時間をさらに縮められれば
その分入手に必要な時間は減ります。
通常のクエストでは敵の湧きや部屋の構造は固定化されているため
次に何が出るか、どこで戦えばよいかなどを把握しておくと
スムーズに進められます。このゲームの醍醐味ですね。
また、RBRや週ブーストによってDARやRDRが増加している場合は
その分必要討伐数が割引されます。
DARが150%、RDRが125%のブーストがかかっている場合、RARは
150% × 125% = 187.5% のブーストがかかるため、
NMU3における周回回数もその分割引され
1つのHS獲得にかかる時間は
46 ÷ 187.5% ≒ 24.5時間 となります。
基本的にRBRではこれらのブーストによって
RBR選出外の優秀なクエストに対抗することが可能となっています。
（中には対抗できない内容のクエストもあるため注意）
マルチの場合は、人が集まるまでの時間も計算に入れておきましょう。
レアエネミーの周回は通常の周回と異なる部分があります。
レアエネミーの出現率は1/500（レアボスであるコンドリューは1/10）であり、
週ボーナスのレアエネミー出現率ブースト期間で出現率が増加します。
一般的にレアエネミーのRARは低めですが、
それはレアエネミーの出現率の低さを加味した上での値になっています。
通常、期待値としてはRARに出現率を掛けた値となります。
つまり、レアエネミーの周回は
・レアエネミーが出現することと
・レアエネミーからレアアイテムが落ちること
の2つの条件を満たす必要があります。
これらが期待値通りに起こるとは限らず、
余事象の計算を用いると
下振れしたときは相当な数の討伐数になると思われます。
例として、紫ミルリリーのサイコウォンドを考えます。
出現率は1/500だからミルリリーが出現するまでの95%信頼値は
500 × 3= 1500体
ミルリリーがサイコウォンドを落とす場合の必要討伐数は
ミルリリーのRARが1/205だから
205 × 3 = 615体
よってリリーの必要討伐数はこれらの積だから
1500×615=922,500体
となります。
通常のエネミー周回とは違い、
レアエネミー出現にも確率が存在するため、必要討伐数は通常の周回の3倍必要になります。
もちろん、95%までにレアエネミーが出現することが多いのでそこまで狩る必要はありませんが、
確率が下振れした場合は通常の周回よりもかなり厳しい事態となりえます。
逆に上振れによってすぐに入手できる可能性もあります。（要するにブレが大きい）
うまくいけばそういうこともありますが、確率は長期的に見れば収束するため過信は禁物。
レアエネミー出現率のブースト値は通常でも150%と
DARやRDRの125%と比べても高めとなっています。
そのため、レアエネミー周回は（当然ながら）レアエネミー出現率ブースト期間に行うのがおすすめです。
レアエネミーの出現率は1/500（レアボスであるコンドリューは1/10）であり、
週ボーナスのレアエネミー出現率ブースト期間で出現率が増加します。
一般的にレアエネミーのRARは低めですが、
それはレアエネミーの出現率の低さを加味した上での値になっています。
通常、期待値としてはRARに出現率を掛けた値となります。
つまり、レアエネミーの周回は
・レアエネミーが出現することと
・レアエネミーからレアアイテムが落ちること
の2つの条件を満たす必要があります。
これらが期待値通りに起こるとは限らず、
余事象の計算を用いると
下振れしたときは相当な数の討伐数になると思われます。
例として、紫ミルリリーのサイコウォンドを考えます。
出現率は1/500だからミルリリーが出現するまでの95%信頼値は
500 × 3= 1500体
ミルリリーがサイコウォンドを落とす場合の必要討伐数は
ミルリリーのRARが1/205だから
205 × 3 = 615体
よってリリーの必要討伐数はこれらの積だから
1500×615=922,500体
となります。
通常のエネミー周回とは違い、
レアエネミー出現にも確率が存在するため、必要討伐数は通常の周回の3倍必要になります。
もちろん、95%までにレアエネミーが出現することが多いのでそこまで狩る必要はありませんが、
確率が下振れした場合は通常の周回よりもかなり厳しい事態となりえます。
逆に上振れによってすぐに入手できる可能性もあります。（要するにブレが大きい）
うまくいけばそういうこともありますが、確率は長期的に見れば収束するため過信は禁物。
レアエネミー出現率のブースト値は通常でも150%と
DARやRDRの125%と比べても高めとなっています。
そのため、レアエネミー周回は（当然ながら）レアエネミー出現率ブースト期間に行うのがおすすめです。
Last edited: